Crypto Shuttle News

Tag: Signatures

  • Threshold Digital Signatures

    Threshold Digital Signatures

    [ad_1]

    By Cassandra Heart, Arash Afshar

    Digital signatures are a foundational concept in blockchain and cryptocurrencies. Modern blockchains use digital signatures to secure billions of dollars of value. Digital signatures use what is known as a keypair, a pair of random looking values, where one key is a “private key” and the other a “public key”. Through digital signatures, any person with the “private key” can “sign” a transaction and spend the digital currencies. Therefore, it is crucial to safeguard the “private key”. Some tech-savvy users of blockchains opt to safeguard this key themselves, and accept the risk of theft or loss of the key (and therefore the loss of their funds). In contrast, other blockchain users trust online wallets or exchanges with the safeguarding of their keys. Of course, this decision comes with its own set of risks based on the competency of the third party.

    In both these options, the user is putting all their trust in a single entity, which may not be desirable. Enter the Threshold Digital Signature: a solution which requires a “threshold” of at least two cooperating participants to produce a signature, and which removes the problem of trusting a single entity. In this article we:

    • Provide an intuitive description of Threshold Signatures and their applications,
    • Dig a bit deeper and look into various Threshold Signature schemes, and
    • Compare Threshold Signatures with other techniques, such as Mulitsig wallets.

    The intuition for threshold signatures

    As a developer in the space of threshold cryptography, it’s really exciting to see these innovations becoming a topic in the mainstream, but readers unfamiliar with cryptography or the math behind it quickly hit roadblocks upon encountering phrases like “Paillier cryptosystem”, “homomorphic encryption” or “Galois field”. It gets even more complicated when you discuss all the moving pieces behind it to coordinate the communication, and as a consequence, very few organizations have been willing to investigate its potential. But it doesn’t have to be scary; at the end, the math comes down to not much more than multiplication and addition. So let’s ELI5: What the heck is a threshold signature?

    In metaphorical terms, signatures are akin to flying a kite on an invisible string. The kite itself is the public key — everyone can see it in the sky. The kite flier moves the kite around by manipulating the invisible string — the private key. The path it takes in the sky as it flies is the signature. Everyone saw the kite fly through the sky in that path, and only through the use of that invisible string was that flight path possible. This feels really simplified compared to the underlying math, but ultimately this metaphor is useful for demonstrating the coordination and work required to make threshold signing possible.

    Enter threshold cryptography. The premise of threshold is literally in its name: some numerical value must be met for an operation to succeed. Oftentimes these processes are defined using the phrase “t of n”, where n is the number of total possible participants, and t is the threshold number that must be met. A common threshold cryptographic scheme that has been used for quite some time is Shamir’s secret sharing scheme. For those unfamiliar, the process involved uses a mathematical technique called Lagrange interpolation to recombine split values into a secret value. In the metaphorical world, it is taking that invisible string, and separating it into individual threads that many people can hold onto, and in order to fly the kite, the threshold number of people must come together and combine their threads into the string again.

    This process works well, and services all over the world use it to secure secret data. The downside is that everyone who is involved must do this process in a secure location when breaking apart and recombining the secret. In cryptocurrencies, this also means that once the private key is recombined and used for signing, it should be considered exposed and all funds held by the key should be moved, so if any participant who helped in recombining the key walks away with it, they can’t do anything meaningful. This is expensive, and not to mention, requires a lot of coordination of people. What if we can take the powerful math behind cryptography and improve upon this so that nobody has to ever meet in a secure location at all?

    The great news is that we can! There are mountains of literature that have risen overnight with new approaches to existing cryptosystems, improvements on previous ones, and completely groundbreaking cryptographic protocols. Navigating this field requires significant time and expertise, but here at Coinbase, we have found and implemented strategies that enable us to leverage these approaches, and support the novel approaches as they are discovered and peer reviewed. There’s a lot involved in this process, so let’s bring it back to the metaphor.

    The setup process for getting our avid kite fliers ready is ultimately the unique twist that enables this entire process to work: each participant follows the same rule: they bring their own invisible thread, and their own piece of kite. Each flier agrees with the others in advance how they are going to fly, and they all proceed to run with their piece of kite at the agreed speed, angle, and time. If anyone strays from the agreed flight plan, the whole tangled mess of kites comes crashing to the ground, but if everyone proceeds as agreed, the kite takes off into one combined piece through the sky, able to perform the flight as planned. When the flight concludes, the parts disassemble mid air, and everyone goes home with their kite and thread. At no point does any one person hold the whole kite or string, and each party sees the flight plan ahead of time to know that nobody is going to try some wild antics that will let them run away with the kite.

    Deeper dive into threshold signatures

    Now that we have an intuitive understanding of threshold signatures, let’s dive deeper into the concepts and terminologies. The threshold signature schemes are part of the secure multi-party computation (MPC) field of cryptography. The main goal of MPC is to enable computation on private data without revealing them to anyone but the owner of the private data. For example, in the kite metaphor, the invisible pieces of the thread are the secret shares of the private key and threshold signature uses these secret shares to reconstruct the private key and sign the transaction without revealing the composite private key, nor the secret shares.

    A very important ingredient of threshold signing is a mathematical construct called Elliptic Curve Cryptography. The TL;DR version is that given `y = x · G`, where `y` and `G` are publicly known values, it is very hard or even impossible to find `x` in a reasonable time frame. There are many “curves” that offer this property:

    • Secp256k1, which is used in Bitcoin, Ethereum and many others
    • Edwards25519, which is used in Cardano, Monero and many others
    • BLS12–381, which is used in Ethereum 2.0 and some other chains

    Given an appropriate elliptic curve, the next step towards a threshold signature is to first choose a standard (i.e., single-signer) digital signature scheme. The popular digital signature schemes are as follows:

    • ECDSA, based on the Secp256k1 curve used by Bitcoin
    • Schnorr, based on the Secp256k1 curve used by Bitcoin Cash and Mina
    • Ed25519, based on the Edwards25519 curve used by Cardano

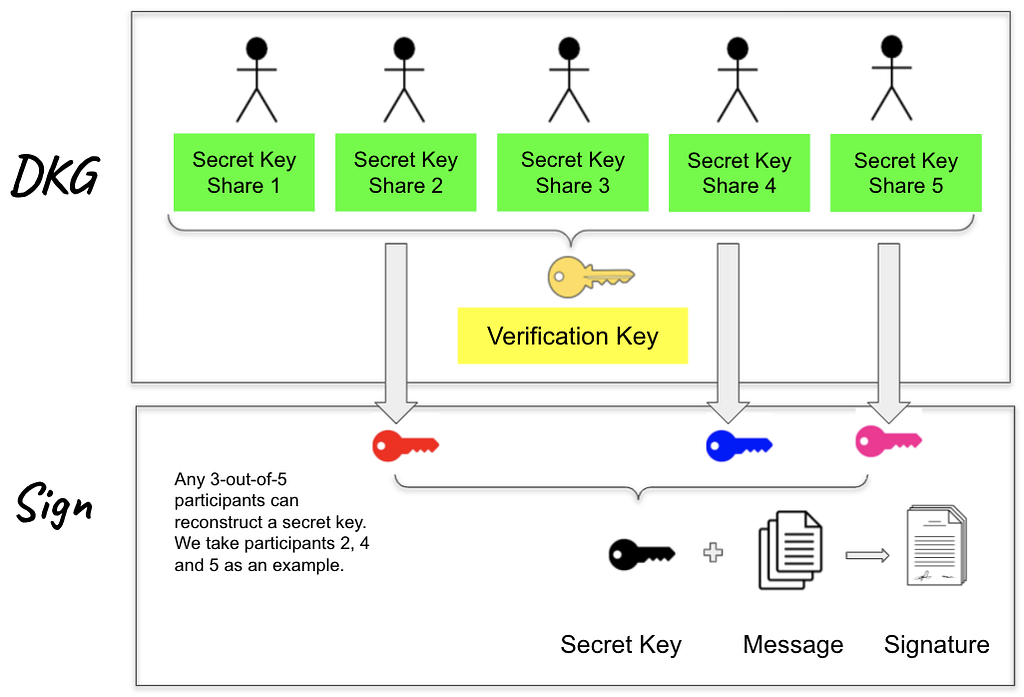
    Finally, given a digital signature we can now discuss threshold signature schemes. The threshold signature schemes start from a single-signer scheme and split the private key between `n` participants. Then, in the signing phase, t-out-of-n participants can run the signing algorithm to obtain the signature. Finally any single (external) party can verify the signature using the same algorithm for verifying the single-signer signatures. In other words, the signatures generated by threshold signature and single-signer signature schemes are interchangeable. Stated differently, a threshold signing algorithm has three phases.

    1. Generate the public/private key pair. Next, split the private key into multiple secret shares and distribute these shares between the `n` parties. This phase can be performed in two modes.
    2. Trusted Dealer mode: A single trusted party will generate the private key, then split and distribute the keys. The main problem with this approach is that the dealer will see the private key in plaintext.
    3. Distributed Key Generation (DKG): an MPC protocol is run between the `n` participants such that at the end, the participants will obtain the secret shares and no one will ever see the private key in plaintext at any point in the process.
    4. Gather a threshold of `t` participants and run an MPC protocol to sign the transaction.
    5. Verify the signature, using the standard signature’s verification algorithm.

    The threshold signature schemes are fast evolving. At the time of writing this post, the secure and popular schemes include the following.

    • FROST is a threshold signature and DKG protocol that offers minimal rounds of communication and is secure to be run in parallel. FROST protocol is a threshold version of the Schnorr signature scheme.
    • DKLs18: is a 2-out-of-2 threshold signature and DKG protocol that offers fast signature computation for ECDSA signature scheme.

    Threshold Signatures and Multisig

    Multisig, or multisignature schemes offer similar capabilities to threshold signatures with a difference: each participant has its own public key (instead of secret shares of a single common public key). This small difference has a huge impact on cost, speed, and availability of the multisig on various blockchains.

    • Efficiency: in threshold signature schemes, each public key, and its corresponding private keyshares, belong permanently to a single, fixed group of signers; in multisignatures, each individual participant has its own distinct, dedicated public key. The benefit of this latter scheme is that each such participant can reuse its private–public keypair to participate in arbitrarily many distinct signing groups. The cost of using multisignatures, however, is that the size of the “public key” (actually, a list of public keys) representing any particular such group must grow linearly in the number of members of that group. Similarly, the verification time of a multisignature obviously must grow linearly in the size of the group, as the verifier must in particular read the entire list of public keys representing the group. In threshold schemes, by contrast, just one public key represents the entire group, and both key-size and verification time are constant.
    • Availability: to ensure that the minimum threshold of `t` is met, the blockchain should have native support for multisignatures. In most cases, this support is in the form of a smart contract. As a result, not all blockchains support multisig wallets. In contrast, the MPC-based threshold signatures are independent of the blockchain as long as the signature scheme that is used by the blockchain has a secure threshold version.

    Final Notes

    Threshold digital signatures enable us to do incredible things previously not possible in cryptocurrencies — multisig contracts require additional costs to operate, but this can happen without a smart contract. This means that we can support a whole new tier of wallets: where before there is the traditional custodial wallet like Coinbase offers in many different ways, or self-custody wallet options like our Coinbase Wallet application, this threshold ECDSA approach allows customers to be an active participant in this signing process. In this approach, the user holds a share of the private key, and Coinbase holds another, and only when both agree to the flight plan, can transactions be signed. This provides the security and trust we are known for at Coinbase, with the user remaining the one in control.

    If you are interested in cutting-edge cryptography, check out our open roles here.

    Threshold Digital Signatures was originally published in The Coinbase Blog on Medium, where people are continuing the conversation by highlighting and responding to this story.

    [ad_2]

    Source link

  • FROST: Flexible Round-Optimized Schnorr Threshold Signatures

    FROST: Flexible Round-Optimized Schnorr Threshold Signatures

    [ad_1]

    By Daniel Zhou

    FROST is a round-optimal threshold Schnorr signature protocol. Here we introduce why Coinbase decided to use FROST, what FROST is, and what we discovered while evaluating FROST.

    Why FROST?

    In order to improve efficiency of Coinbase’s threshold-signing systems, we decided to explore the FROST threshold Schnorr signature protocol, which features the following advantages over other Schnorr-based threshold signature protocols [GJKR03, SS01]:

    Low round complexity in both the distributed key-generation and signing phases. The distributed key generation phase can be completed in 2 rounds. The signing phase can be completed in less or equal to 3 rounds depending on whether we use a signature aggregator role and a preprocessing stage. That is,

    • 1-round signing with a trusted signature aggregator and a preprocessing stage.
    • 2-round signing with a trusted signature aggregator, but no preprocessing stage.
    • 3-round signing without a trusted signature aggregator and no preprocessing stage.

    Concurrent security. The signing phase is secure when performed concurrently. That is, an unlimited number of signature operations can be performed in parallel. In contrast with other threshold Schnorr signature protocols, there are existing Schnorr-based threshold signature protocols, such as [GJKR03, SS01], that have the same round complexity, but they suffer from limited concurrency to protect against the attack of Drijvers et al. [DEF19]. This attack was originally proposed in a Schnorr multi-signature n-out-of-n setting, but it also applies similarly in a threshold t-out-of-n setting with the same parameters for an adversary that controls up to t-1 participants. We refer readers to section 2.6 of the FROST draft for more details. To prevent this attack without limiting concurrency, FROST binds each participant’s response to a specific message as well as the set of participants and their set of elliptic curve (EC) points used for that particular signing operation. In doing so, combining responses over different messages or EC point pairs results in an invalid signature, thwarting attacks such as those of Drijvers, et al.

    Secure against dishonest majority. FROST is secure against adversaries which control up to t-1 signers in the signing phase.

    Simple cryptographic building blocks and assumptions. FROST is built upon the threshold Shamir secret sharing and Feldman verifiable secret sharing schemes and it relies only on the discrete logarithm assumption.

    How does FROST work?

    Before we introduce how FROST works, we first recall how the standalone Schnorr signature works.

    A Schnorr digital signature algorithm is a triple of algorithms: (KeyGen, Sign, Verify).

    Let G be a group generator of a cyclic group with prime order p, and let H be a cryptographic hash function mapping to the field Zₚ* . A Schnorr signature is generated over a message m by the following steps:

    KeyGen -> (sk, vk)

    • Randomly sample the secret key sk <- Zₚ.
    • Return (sk, vk = sk * G).

    Sign(sk, m) -> sig

    • Randomly sample a secret nonce k <- Zₚ.
    • R = k * G
    • c = H(m, R)
    • z = k + sk * c (mod p)
    • Return signature sig = (z, c)

    Verify(vk, m, sig) -> true/false

    • Parse sig = (z’, c’)
    • R’ = z * G -c * vk
    • c’ = H(m, R’)
    • Return true if c = c’, otherwise return false.

    We call (sk, vk) the secret and verification keys respectively. We call m the message being signed and sig the Schnorr digital signature.

    FROST is a threshold Schnorr signature protocol that contains two important components. First, n participants run a distributed key generation (DKG) protocol to generate a common verification key; at the end, each participant obtains a private secret key share and a public verification key share. Afterwards, any t-out-of-n participants can run a threshold signing protocol to collaboratively generate a valid Schnorr signature. The figure below gives a high-level sketch of how FROST works in the case of t = 3 and n = 5.

    (3, 5) — FROST DKG + Threshold Signing Overview

    In the following context, we introduce FROST distributed key generation and threshold signing in more technical details.

    FROST — distributed key generation (DKG). The secret signing key in Schnorr signature is an element in the field Zₚ. The goal of this phase is to generate long-lived secret key shares and a joint verification key. This phase is run by n participants. FROST builds its own key generation phase upon Pedersen’s DKG [GJKR03], in which it uses both Shamir secret sharing and Feldman’s verifiable secret sharing schemes as subroutines. In addition, FROST also requires each participant to demonstrate knowledge of their own secret by sending to other participants a zero-knowledge proof, which itself is a Schnorr signature. This additional step protects against rogue-key attacks in the setting where t ≥ n/2.

    At the end of the DKG protocol, a joint verification key vk is generated. Also, each participant Pᵢ holds a value (i, skᵢ) that is their long-lived secret share and a verification key share vkᵢ = skᵢ*G. Participant Pᵢ’s verification key share vkᵢ is used by other participants to verify the correctness of Pᵢ’s signature shares in the signing phase, while the verification key vk is used by external parties to verify signatures issued by the group.

    FROST — threshold signing. We now introduce the signing protocol for FROST. This phase builds upon known techniques that employ additive secret sharing and share conversion to non-interactively generate the nonce for each signature. This phase also leverages binding techniques to avoid known forgery attacks without limiting concurrency.

    Our implementation is slightly adapted from the FROST draft. In our implementation, we opted to not use the signature aggregator role. Instead, each participant is a signature aggregator. This design is more secure: all the participants of the protocol verify what others have computed to achieve a higher level of security and reduce risk. In contrast with other open source libraries, as far as we know, we are the first to implement FROST without the signature aggregator role. Furthermore, we have chosen not to do the (one-time) preprocessing stage in order to speed up the implementation. In the preprocessing stage, each participant prepares a fixed number of EC point pairs for further use, which is run for a single time for multiple threshold signing phases. However, we take this stage as an additional round and only prepare a single pair of EC points, which means we run it every time for each threshold signing phase. In more detail, there are two major differences between our implementation and the original draft.

    First, the signature aggregator, as described in the draft, validates messages that are broadcast by cosigners and computes the final signature. In our implementation, we do not use such a role. Instead, each participant simply performs a broadcast in place of a signature aggregator performing coordination. Note that FROST can be instantiated without such a signature aggregator as stressed in the draft. Also, implementing it in a decentralized way is more appropriate to Coinbase’s multiparty computation approach.

    Second, the protocol in the draft uses a preprocessing stage prior to signing, where each participant Pᵢ samples a sequence number, say Q, of single-use nonces (dᵢⱼ, eᵢⱼ), computes and broadcasts pairs of public points (Dᵢⱼ = dᵢⱼ*G, Eᵢⱼ = eᵢⱼ*G) for further use in subsequent signing rounds, where j = 1….Q. This preprocessing stage is a once-for-all stage. That is, each participant can prepare a fixed number of EC point pairs, say Q, and broadcast them to the signature aggregator, then the signature aggregator distributes these EC point pairs to all participants for further use. Once these pairs of EC points are used up, then these participants should run another preprocessing stage. Since we opted to not use such a signature aggregator role in our implementation, we have chosen instead to let each participant generate a single pair of EC points (Dᵢ, Eᵢ). Therefore, there is no preprocessing stage in our implementation and thus there are 3 rounds in our threshold signing phase instead of 2. Also note that whether our implementation contains the preprocessing stage or not simply depends on how many EC point pairs are generated in signing round 1. If each participant generates a Q number of EC point pairs in the signing round 1, then this round can be viewed as the preprocessing stage and our implementation becomes a 2-round signing protocol.

    We describe how these three signing rounds work and give some technical details.

    Signing Round 1. Each participant Pᵢ begins by generating a single private nonce pair (dᵢ, eᵢ) and corresponding pair of EC points (Dᵢ, Eᵢ) and broadcasts this pair of points to all other participants. Each participant stores these pairs of EC points received for use later. Signing rounds 2 and 3 are the actual operations in which t-out-of-n participants cooperate to create a valid Schnorr signature.

    Signing Round 2. To create a valid Schnorr signature, any t participants work together to execute this round. The core technique behind this round is t-out-of-t additive secret sharing. This technique creates the secret nonce k = SUM(kᵢ), which is the same value generated in the single-party Schnorr signing algorithm, and each kᵢ is the share computed by participant Pᵢ. To do this, each participant prepares the set of pairs of EC points B = (D₁, E₁)……(Dₜ, Eₜ) received in round 1, and then computes kᵢ = dᵢ+eᵢ*rᵢ , where rᵢ=H(i, m, B) and H is a hash function whose outputs are in the field Zₚ. Computing rᵢ is important since it works as a binding value for each participant to prevent the forgery attack. Then each participant computes the commitment Rᵢ=Dᵢ+Eᵢ*rᵢ such that it binds the message m, the set of signing participants and each participant’s EC points to each signature share, such that signature shares for one message cannot be used for another. This prevents the forgery attack because attackers cannot combine signature shares across distinct signing operations or permute the set of signers or published points for each signer. The commitment for the set of signers is then simply R = SUM(Rᵢ). As in single-party Schnorr signatures, each participant computes the challenge c = H(m, R).

    Having computed the challenge c, each participant is able to compute the response zᵢ to the challenge using the single-use nonces (dᵢ, eᵢ) and the long-term secret shares skᵢ, which are t-out-of-n (degree t-1) Shamir secret shares of the group’s long-lived key sk. One main observation that FROST leverages is that if kᵢ are additive shares of k, then each kᵢ/Lᵢ are t-out-of-n Shamir shares of k, where Lᵢ is the Lagrange coefficient for participant Pᵢ. That is, Lᵢ = prod(i/(j-i)), where j = 1,…,t, j ≠i. This observation is due to the work by Benaloh and Leichter [BL88] and the work by Cramer, Damgaard and Ishai [CDI05]. They present a non-interactive mechanism for participants to locally convert additive shares generated via the Benaloh and Leichter t-out-of-n secret sharing construction to Shamir’s polynomial form. FROST uses the simplest t-out-of-t case of this transformation. Thus kᵢ/Lᵢ+skᵢ*c are degree t-1 Shamir secret shares of the correct response z = k+sk*c for a plain (single-party) Schnorr signature. Using share conversion again and the value each participant has computed (namely, kᵢ = dᵢ+eᵢ*rᵢ), we get that zᵢ=dᵢ+eᵢ*rᵢ+Lᵢ*skᵢ*c are t-out-of-t additive shares of z. At the end of signing round 2, each participant broadcasts zᵢ to other participants.

    Signing Round 3. After receiving zᵢ from all other participants, each participant checks the consistency of these reported zᵢ, with their pair of EC points (Dᵢ, Eᵢ) and their verification key share vkᵢ. This can be done by checking the equation zᵢ*G = Rᵢ+c*Lᵢ*vkᵢ. Once all zᵢ are valid, then each participant computes z = SUM(zᵢ) and output (z, c) as the final Schnorr signature. This signature will verify properly to any party unaware that FROST was used to generate the signature, and can check it with the standard single-party Schnorr verification equation with vk as the verification key. As we have mentioned, we do not use the signature aggregator role in our implementation. Thus, each participant works as a signature aggregator. Therefore, we let each participant self-verify its own signature before outputting it.

    Implementation Challenges

    We referred to some known FROST implementations: two Rust implementations — one by ZCash foundation and another by frost-dalek — but they are not appropriate to our tech stack. One Golang implementation is from the Taurus group, but unfortunately this Go implementation is not ready for production use and has not been externally audited. As a result, we decided to implement the protocol in-house.

    One feature of FROST signing is that each participant must know Lagrange coefficients for each participant in order to compute zᵢ. This is uncommon in other threshold signature protocols that use Feldman verifiable secret sharing as a sub-protocol, so there are few existing Go libraries to support THIS. Most existing libraries support generating secret shares, polynomials, and their interpolation, but do not support Lagrange coefficient computation. To fill in this technical gap, we implemented participants’ Lagrange coefficients given arbitrary t participant IDs as input. Before running the threshold signing protocol, it takes input IDs of the t participants and generates all Lagrange coefficients. As the FROST draft suggests, we assign these coefficients to each participant before signing to improve performance.

    Summary

    FROST is a flexible, round-optimized Schnorr threshold signature scheme that minimizes the network overhead of producing Schnorr signatures in a threshold setting while allowing for unrestricted parallelism of signing operations and only a threshold number of signing participants. We introduce FROST, highlight its features, and describe it in a fully decentralized approach (i.e., without any third-party signature aggregator). This post exposes what Coinbase discovered while evaluating and implementing the FROST protocol and we look forward to adding it to our suite of threshold signing services.

    If you are interested in cutting-edge cryptography, Coinbase is hiring.

    FROST: Flexible Round-Optimized Schnorr Threshold Signatures was originally published in The Coinbase Blog on Medium, where people are continuing the conversation by highlighting and responding to this story.

    [ad_2]

    Source link